Lineas de Bézier

LINEAS DE BÉZIER

Se denomina curvas de Bézier a un sistema que se desarrolló hacia los años 1960 para el trazado de dibujos técnicos, en el diseño aeronáutico y en el de automóviles. Su denominación es en honor a Pierre Bézier, quien ideó un método de descripción matemática de las curvas que se comenzó a utilizar con éxito en los programas de CAD.

Curvas lineales de Bézier

Dados los puntos P0 y P1, una curva lineal de Bézier es una línea recta entre los dos puntos. La curva viene dada por la expresión: {{B} (t)= {P} _{0}+{P} _{1}-{P} _{0})t=(1-t){P} _{0}+{P} _{1}{ [0,1].}

Curvas cuadráticas de Bézier 

Una curva cuadrática de Bézier es el camino trazado por la función B(t), dados los puntos: P0, P1, y P2,

{{B} (t)=(1-t)^{2}\P} _{0}+2t(1-t)\ {P} _{1}+t^{2{P} _{2}{[0,1].}

Curvas cúbicas de Bézier

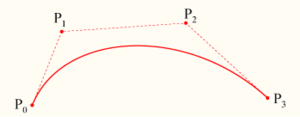
Curva cúbica de Bézier donde se aprecian los puntos o nodos de anclaje P1 y P2.

Cuatro puntos del plano o del espacio tridimensional, P0, P1, P2 y P3 definen una curva cúbica de Bézier. La curva comienza en el punto P0 y se dirige hacia P1 y llega a P3 viniendo de la dirección del punto P2. Usualmente, no pasará ni por P1 ni por P2. Estos puntos solo están ahí para proporcionar información direccional. La distancia entre P0 y P1 determina "qué longitud" tiene la curva cuando se mueve hacia la dirección de P2 antes de dirigirse hacia P3.

VIDEO

GEOGEBRA Y LIBRETA